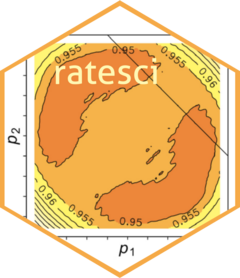
Score confidence intervals for a single binomial rate from clustered data.

Asymptotic Score confidence intervals for a proportion estimated from a clustered sample, as decribed by Saha et al. 2016. With optional skewness correction to improve interval location (to be evaluated).

Usage

clusterpci(x, n, level = 0.95, skew = TRUE, cc = FALSE, theta0 = 0.5)

Arguments

x: Numeric vector of number of events per cluster.
n: Numeric vector of sample sizes per cluster.
level: Number specifying confidence level (between 0 and 1, default 0.95).
skew: Logical (default TRUE) indicating whether to apply skewness correction or not. (To be evaluated)
cc: Number or logical (default FALSE) specifying (amount of) continuity adjustment. Numeric value is taken as the gamma parameter in Laud 2017, Appendix S2 (default 0.5 for 'conventional' adjustment if cc = TRUE).
theta0: Number to be used in a one-sided significance test (e.g. non-inferiority margin). 1-sided p-value will be <0.025 iff 2-sided 95\ excludes theta0.

Value

A list containing the following components:

estimates: the estimate and confidence interval for p and the specified confidence level, along with estimates of the ICC and the variance inflation factor, xihat.
pval: one-sided significance tests against the null hypothesis that theta >= or <= theta0 as specified.
call: details of the function call.

References

Saha K, Miller D and Wang S. A comparison of some approximate confidence intervals for a single proportion for clustered binary outcome data. Int J Biostat 2016; 12:1–18

Short MI et al. A novel confidence interval for a single proportion in the presence of clustered binary outcome data. Stat Meth Med Res 2020; 29(1):111–121

Author

Pete Laud, p.j.laud@sheffield.ac.uk

Examples

  # Data example from Liang 1992, used in Saha 2016 and Short 2020:
  # Note Saha states the ICC estimate is 0.1871 and Short makes it 0.1855.
  # I agree with Short - CI limits differ from Saha to the 4th dp.
  x <- c(rep(c(0, 1), c(36, 12)),
         rep(c(0, 1, 2), c(15, 7, 1)),
         rep(c(0, 1, 2, 3), c(5, 7, 3, 2)),
         rep(c(0, 1, 2), c(3, 3, 1)),
         c(0, 2, 3, 4, 6))
  n <- c(rep(1, 48),
         rep(2, 23),
         rep(3, 17),
         rep(4, 7),
         rep(6, 5))
  # Wilson-based interval
  clusterpci(x, n, skew = FALSE)
#> $estimates
#>          lower       est     upper totx totn    xihat       icc
#> [1,] 0.2284814 0.2955665 0.3728302   60  203 1.349133 0.1855342
#> 
#> $pval
#>      theta0 scorenull    pval_left pval_right
#> [1,]    0.5 -5.015366 2.646631e-07  0.9999997
#> 
#> $call
#>   level    skew      cc 
#>  "0.95" "FALSE" "FALSE" 
#> 
  # Skewness-corrected version
  clusterpci(x, n, skew = TRUE)
#> $estimates
#>          lower      est     upper  x   n totx totn    xihat       icc
#> [1,] 0.2276278 0.295815 0.3723694 60 203   60  203 1.349133 0.1855342
#> 
#> $pval
#>      theta0 scorenull    pval_left pval_right
#> [1,]    0.5 -5.015366 2.646631e-07  0.9999997
#> 
#> $call
#>   level    skew      cc 
#>  "0.95"  "TRUE" "FALSE" 
#> 
  # With continuity adjustment
  clusterpci(x, n, skew = FALSE, cc = TRUE)
#> $estimates
#>          lower       est     upper totx totn    xihat       icc
#> [1,] 0.2262502 0.2955665 0.3754001   60  203 1.349133 0.1855342
#> 
#> $pval
#>      theta0 scorenull    pval_left pval_right
#> [1,]    0.5 -4.894514 4.927455e-07  0.9999995
#> 
#> $call
#>   level    skew      cc 
#>  "0.95" "FALSE"  "TRUE" 
#>